Standard Error
In the previous two chapters you've seen that we can often predict the behavior of the null distribution using mathematical theory instead of simulation as long as certain validity conditions are met. We will now explore a theory-based approach for testing a single mean. As it turns out people typically don't predict the distribution of sample means directly, instead they predict the distribution of the standardized statistic. The process of standardizing the statistic is the same as before: (observed statistic - mean of null distribution)/(SD of null distribution).
However, it is more problematic that we don't really know the population standard deviation. We can use the sample standard deviation s to approximate the population standard deviation. Then we approximate the standard deviation of the sample means by 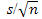 . This approximation to the standard deviation of the sampling distribution is called the standard error of the sample mean.
. This approximation to the standard deviation of the sampling distribution is called the standard error of the sample mean.
(k) Calculate the standard error for our class data. (Show your work.)
(l) Use the standard error to standardize the observed sample mean compared to the assumed population mean: (observation - mean)/standard error. [You will interpret this just like before, how many standard errors is the observed statistic from the hypothesized parameter value.] (Show your work.)
(m) Based on what you learned about standardized statistics in Ch. 1, does this value provide evidence against the null hypothesis? Explain.

